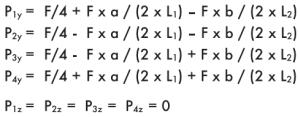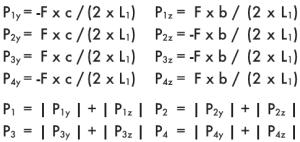Линейные направляющие
 Профильные рельсовые направляющие серии LLT
Профильные рельсовые направляющие серии LLT
 Профильные рельсовые направляющие LLR
Профильные рельсовые направляющие LLR
 Миниатюрные рельсовые линейные направляющие
Миниатюрные рельсовые линейные направляющие

 |
Основные характеристики каретки:
|
 |
Основные характеристики каретки:
|
 |
Основные характеристики каретки:
|
 |
Основные характеристики каретки:
|
 |
Основные характеристики каретки:
|
 |
Основные характеристики каретки:
|
|
|
Основные характеристики каретки:
|
|
|
Основные характеристики каретки:
|
|
|
Серия SLA >>
|
|
|
Основные характеристики каретки:
|
|
|
Основные характеристики каретки:
|
|
|
Основные характеристики каретки:
|
|
|
Серия RLC >>
|
|
|
Серия RSC >>
|
|
|
Серия RNX; RLX >>
|
|
|
Маслянные баки для систем линейного перемещения >>
|
|
|
Принадлежности для систем линейного перемещения >>
|
2. Выбор системы линейного перемещения NBS
Тип линейной системы с профильными направляющими (направляющая + каретка) выбирается на основании следующих параметров:
• Применяемая нагрузка
• Требуемый срок службы
• Габаритные размеры
• Скорость
• Цикл работы
• Точность
• Жесткость
3. Нагрузочная способность и срок эксплуатации
Показатели, применяемые для определения способности линейной системы на поглощение нагрузок и (или) статических моментов использовали следующие величины:
• Статическая нагрузочная способность С0
• Статический допустимый момент М0
3.1 Статическая нагрузка
Нагрузочная статическая способность С0 (или коэффициент нагрузочной способности) определяется в качестве интенсивной статической нагрузки в зависимости от постоянного направления, определяющего, в точке максимального воздействия между соприкасающимися частями, остаточную деформацию, равную 1/10000 диаметра тела качения.
Статическая нагрузочная способность С0 линейной системы с профильными направляющими ограничивается следующими параметрами:
• Допустимая нагрузка направляющей
• Нагрузочная способность дорожек качения
• Допустимая нагрузка крепежных винтов
• Требуемый коэффициент статического запаса прочности
Значения С0 приведены в размерных таблицах.
3.1.1 Статический допустимый момент М0 ш
Допустимый статический момент М0 определяется статическим моментом интенсивности и постоянного направления, определяющего, в точке максимального воздействия между поверхностями соприкосновения, пластическую деформацию равную 1/10000 диаметра тела качения; в этом случае, точками максимального воздействия становятся точки соприкосновения между телами качения и направляющей, расположенными по краям каретки.
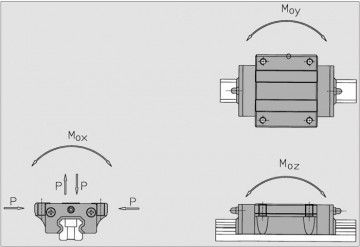
Допустимый статический момент М0 рассчитан для трех картезианских осейх, y z (из которых: Мох, M0Y, Moz).
Для допустимого статического момента являются действительными ограничения, вызванные вследствие:
• допустимой нагрузки
• нагрузочной способности дорожек качения
• допустимой нагрузки крепежных винтов
• требуемого коэффициента статического запаса прочности
Значения Мох, M0Y, Moz приведены в размерных таблицах.
3.1.2 Коэффициент статического запаса прочности as 1
Коэффициент статического запаса прочности as (или фактор статического запаса прочности) определяет соотношение между нагрузочной способностью Со и применимой эквивалентной нагрузкой Р или, соотношение между допустимым статическим моментом Мо (Мох, Moy, Moz) и применимым моментом М (Мх, My, Mz); при соотношении нужно учитывать моменты на одной оси.
![]()
где:
- as = коэффициент статического запаса прочности
- fc = коэффициент контакта
- Со = нагрузочная статическая способность
- [N] Р = эквивалентная воздействующая нагрузка [N] (см. "Расчет воздействующей нагрузки")
- Мох = допустимый статический момент на оси х [Nx m]
- M0Y = допустимый статический момент на оси y[Nxm]
- Moz = допустимый статический момент на оси z[Nxm]
- Мх = воздействующий момент на оси x[Nxm]
- My = воздействующий момент на оси y[Nxm]
- Mz = воздействующий момент на оси z[Nxm]
3.1.3 Коэффициент контакта fc
Если два или больше блоков устанавливаются на одной направляющей, то долговечность сокращается из-за неполной однородности распределения воздействующих нагрузок на блоки.
|
Количество блоков на одной направляющей |
fc |
| 1 | 1.0 |
| 2 | 0.81 |
| 3 | 0.72 |
| 4 | 0.66 |
| 5 | 0.61 |
Необходимость в коэффициенте статического запаса прочности as > 1 вызвана возможным наличием ударов и (или) вибраций, пусковых и остановочных моментов, случайных нагрузок, которые могут привести к неисправности системы.
В таблице отображены минимальные ориентировочные значения для коэффициента статического запаса прочности as.
Таблица - Коэффициент статического запаса прочности as
| Условия эксплуатации | минимальные as |
| Статическое | 1.0-2.0 |
| Динамическое | 2.0-4.0 |
| Динамическое с ударами и вибрацией | 3.0-5.0 |
Показатель, используемый для определения способности линейной системы поглощать воздействующие динамические нагрузки, заключается в динамической нагрузочной способности С.
3.2 Динамическая нагрузка
Нагрузочной динамической способностью С (или коэффициентом динамической нагрузки) является та интенсивная динамическая нагрузка и постоянное направление, определяющее номинальную продолжительность равную 50 км расстояния; под продолжительностью подразумевается теоретическое расстояние без признаков усталости материала.
Динамическая нагрузочная способность С линейной системы с профильными направляющими ограничивается следующими параметрами:
• Скорость эксплуатации
• Эксплуатационный цикл
• Воздействующие нагрузки и (или) моменты
Значения С приведены в размерных таблицах. (Согласно стандарту DIN нагрузочная динамическая способность С должна быть в два раза больше воздействующей эквивалентной нагрузки Р).
3.3 Срок службы L
Номинальный ресурс L для систем линейного перемещения с циркуляцией шариков (это теоретический пробег, выполненный, по крайней мере, 90% показательного количества одинаковых шариковых подшипников не проявляя признаков усталости материала) рассчитывается следующим уравнением:
![]()
где:
L = номинальный ресурс [км]
С = нагрузочная динамическая способность [N]
Р = эквивалентная воздействующая нагрузка [N]
Данное уравнение действительно в следующих случаях:
• Температура дорожки качения < 100 °С
• Твердость дорожек качения > 58 HRC
• Отсутствие ударов и вибрации
• Скорость скольжения < 15 м/мин
• Один блок на направляющий рельс, fc=1
В том случае, если условия эксплуатации не соответствуют приведенным выше условиям, следует использовать следующую формулу:
![]()
где:
L = номинальный ресурс [км]
a1 = коэффициент надежности
Fh = коэффициент твердости
h = коэффициент температуры
fc = коэффициент контакта
fw = коэффициент нагрузки
С = нагрузочная динамическая способность [N]
Р = эквивалентная воздействующая нагрузка [N]
Ниже приводятся определения коэффициентов at, fn, h, fw.
3.3.1 Коэффициент a1
Коэффициент а 1 рассчитывает процент возможности непрогиба
Таблица - Коэффициент возможности не прогиба a1
|
с% |
80 |
85 |
90 |
92 |
95 |
96 |
97 |
98 |
99 |
|
a1 |
1.96 |
1.48 |
1.00 |
0.81 |
0.62 |
0.53 |
0.44 |
0.33 |
0.21 |
Следует заметить, что для С% = 90, a1 = 1.00.
3.3.2 Коэффициент твердости fh
Твердость контактной поверхности дорожки ниже 58 HRC способствует явлению износа и, соответственно, сокращению номинального ресурса системы.
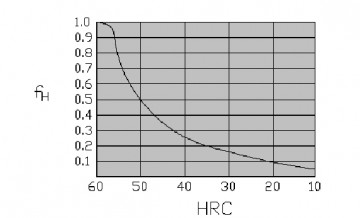
3.3.3 Температурный коэффициент fh
Необходимо знать температуру окружающей среды системы, т.к. значение, превышающее 100°С, может изменить свойства материалов с последующим сокращением номинального ресурса.
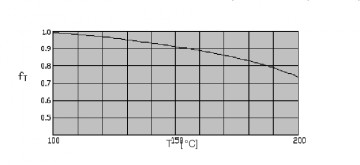
3.3.4 Коэффициент нагрузки fw
В том случае, если нет возможности точно рассчитать все возлагаемые динамические нагрузки, такие как, например, сила инерции и соответствующие опрокидывающие моменты, вибрация и удары, вызванные, как правило, высокими скоростями, такие явления должны учитываться с помощью данного коэффициента.
Таблица - Коэффициент нагрузки fw
|
Рабочие условия |
Измеренная вибрация |
fw |
|
Отсутствие ударов и вибрации и (или) низкая скорость (v< 15 m/min) |
G<0,5 |
1.0-1.5 |
|
Отсутствие легких ударов и вибрации и (или) средняя скорость (15 < v < 60 m/min) |
0,5 <G< 1,0 |
1.5-2.0 |
|
Отсутствие сильных ударов и вибрации и (или) высокая скорость (v > 60 m/min) |
1,0<G<2,0 |
2.0-3.5 |
Эффективный ресурс Lett (или срок эксплуатации) может отличаться от рассчитанного номинального L, так как он зависит и от следующих факторов:
• Окружающая среда (наличие пыли и (или) окисляющих веществ)
• Смазка
• Монтаж направляющих (возможные смещения)
• Преднатяг
3.3.5 Срок службы Lh
Зная L (номинальный ресурс пройденного расстояния в км)
можно определить срок эксплуатации в часах (Lh).
Срок эксплуатации можно определить в следующих условиях:
• Постоянная скорость
• Переменная скорость
Постоянная скорость
Срок эксплуатации в часах Lh - это функция длины пройденного пути и количества переменных циклов в минуту; определяется по формуле:
![]()
где:
Lh = продолжительность эксплуатации [часы] L = номинальный ресурс [км] lc = длина хода [м]
n alt = к-во переменных циклов в минуту [min-1] Переменная скорость
Срок эксплуатации в часах Lh - функция средней скорости
![]()

3.3.6 Сопротивление трению
Расчет сопротивления трению S проводится с помощью следующей формулы:
![]()

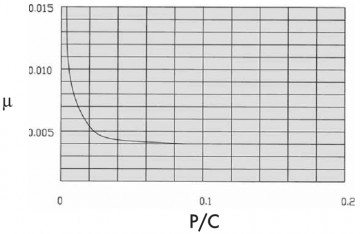
- Р = эквивалентная воздействующая нагрузка [N]
- С = нагрузочная динамическая способность [N]
Трение прокладок f
Таблица - Трение прокладок на блок
|
Размер блока |
f |
|
15 |
3.1 N |
|
20 |
3.9 N |
|
25 |
4.4 N |
|
30 |
5.4 N |
|
35 |
7.4 N |
|
45 |
9.1 N |
|
55 |
10.2 N |
4. Расчет применяемой нагрузки
Для лучшего понимания расчетов касающихся действующих нагрузок, используется буква F для указания общих воздействующих на структуру нагрузок и буква Р, для указания нагрузок, воздействующих на направляющие.
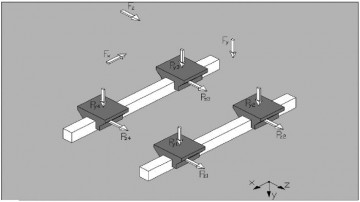
Учитывая переменность действующих нагрузок, рассчитывается новое значение постоянной нагрузки, так называемая "средняя эквивалентная динамическая нагрузка Pm" которая, с целью получения расчетов о сроке службы системы, определяет одинаковые воздействия переменных действующих нагрузок. Для расчета срока службы L нужно учитывать:
Pm = Р
4.1 Эквивалентная средняя динамическая нагрузка
При условиях ступенчато изменяющейся нагрузки и постоянной скорости:
![]()

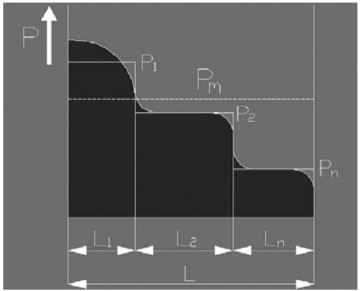
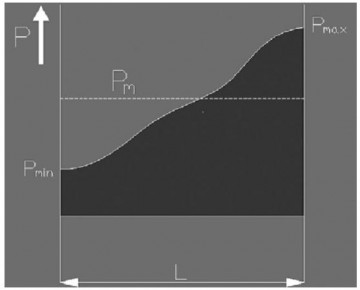
При условиях линейно изменяющейся нагрузки и постоянной скорости:
![]()
где:
- Рm = эквивалентная средняя динамическая нагрузка [N]
- P min = минимальная нагрузка [N]
- P max = максимальная нагрузка [N]
При условиях постепенно изменяющейся нагрузки и постоянной скорости: Pm=0.65 Pmax
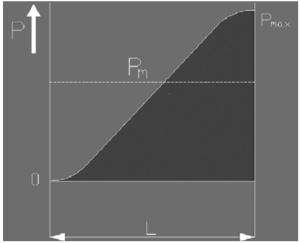
Pm=0.75 Pmax
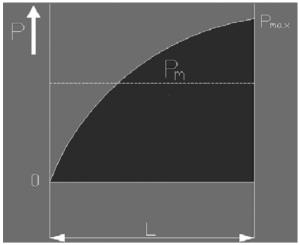
где:
Pm = эквивалентная средняя динамическая нагрузка [NJ]
Рmax =максимальная нагрузка [NJ]
При условиях постепенно изменяющейся нагрузки и постоянной скорости:
![]()
где:
Pm = эквивалентная средняя динамическая нагрузка [NJ]
qn = энное процентное распределение [%]
Рп = энная нагрузка [NJ]
vn = энная скорость [м/мин]
В любом случае, следует учитывать, что
Pm=Рmax
Нагрузки в разных направлениях
Для расчета нагрузок, действующих в двух основных направлениях у и z нужно суммировать их модули:
(для удобства, используется буква Р с целью определения средней эквивалентной динамической нагрузки)
где:
P = эквивалентная воздействующая нагрузка [N]
Py— нагрузка, действующая в направлении у [N]
Pz = нагрузка, действующая в направлении z [N]
4.2 Примеры расчетов для самых распространенных применений
Девять приведенных ниже примеров становятся отображением осуществления расчета нагрузок, действующих для самых распространенных применений систем линейного перемещения данного типа.
Пример 1
Монтаж на горизонтальной поверхностиг, одна направляющая, два ползуна, консольная нагрузка, отсутствие сил инерции.
 |
a = расстояние x между силой F и центром ползунов
b = расстояние z между силой F и направляющей осью
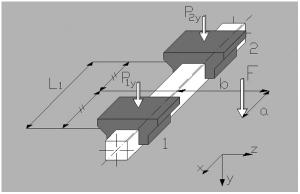
Пример 2
Монтаж на горизонтальной поверхности, двойная направляющая, четыре ползуна, отсутствие сил инерции.
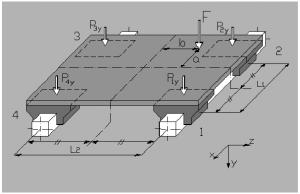
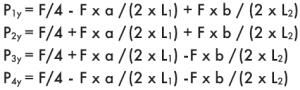
a = расстояние x между силой F и основной осью
b = расстояние z между силой F и основной осью
Пример 3
Монтаж на горизонтальной поверхности, двойная направляющая, четыре ползуна, консольная нагрузка, отсутствие сил инерции.
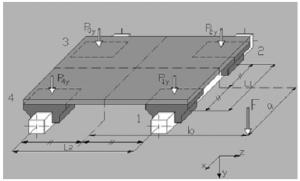 |
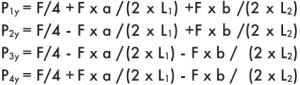 |
a = расстояние x между силой F и основной осью
Ь = расстояние z между силой F и основной осью
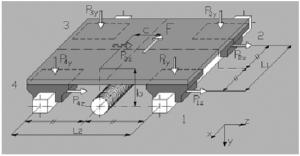
Пример 4
Монтаж на горизонтальной поверхности, двойная направляющая, четыре ползуна, нагрузка в направлении х, отсутствие сил инерции.
 |
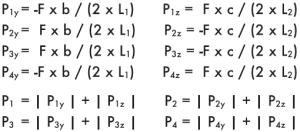 |
b = растояние y между силой А и основной осью
c = растояние z между силой А и основной осью
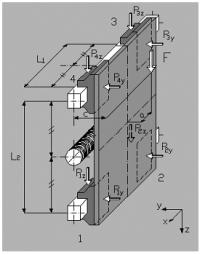
Пример 5
Монтаж на вертикальной поверхности с горизонтальным ходом, двойная направляющая, четыре ползуна, отсутствие сил инерции.
 |
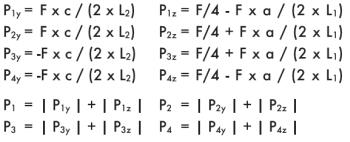 |
a = расстояние x между силой Fи основной осью
с = расстояние z между силой Fи основной осью
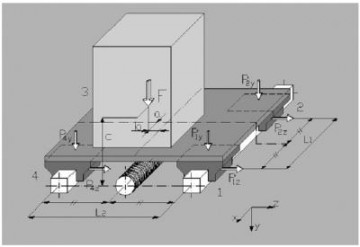
Пример 6
Монтаж на горизонтальной поверхности, двойная направляющая, четыре ползуна, наличие сил инерции.
 |
Движение постоянной в покое:
|
При ускорении:
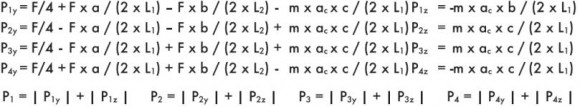
При замедлении:
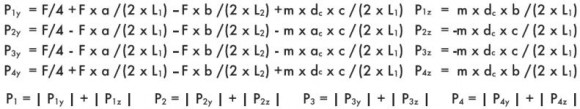
F = нагрузка, действующая в центре тяжести
m = F/9,81
ас = ускорение (скорость/времяускорения)
dc = замедление (скорость/время замедления)
а = расстояние х между силой F и основной осью
b = расстояние z между силой F и основной осью
с = расстояние у между силой F и основной осью
(формулы относятся к движению, касающемуся оси х; в случае иного движения, следует переставить все факторы, содержащие термин m).
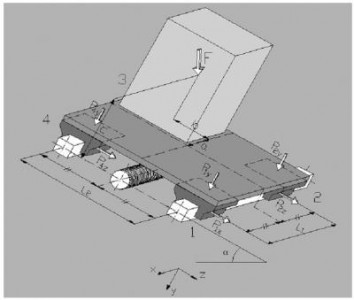
Пример 7
Монтаж на наклонной поверхности (вращение оси х), двойная направляющая, четыре ползуна, отсутствие сил инерции.
 |
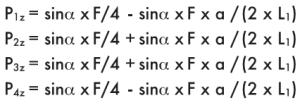 |
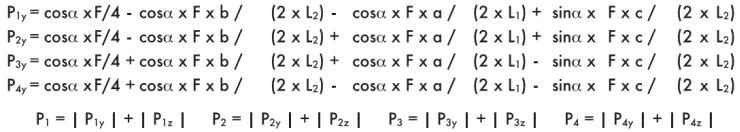
F = нагрузка, действующая в центре тяжести
а = расстояние х между силой F и основной осью
b = расстояние z между силой F и основной осью
с = расстояние у между силой F и основной осью
Пример 8
Монтаж на вертикальной поверхности с вертикальным ходом, двойная направляющая, четыре ползуна, наличие сил инерции.
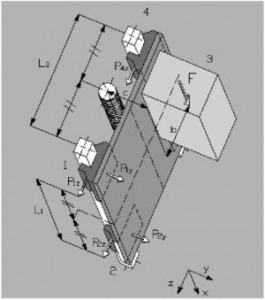 |
Движение с постоянной скоростью или в состоянии покоя:
|
При ускорении:
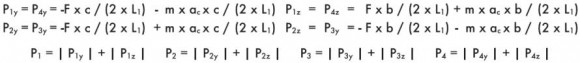
При замедлении:
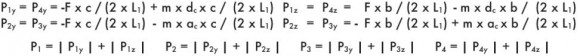
F = нагрузка, действующая в центре тяжести
m = Ft 9,81
ас = ускорение (скорость/время ускорения)
dc = замедление (скорость/время замедления)
b = расстояние z между силой F и основной осью
с = расстояние у между силой F и основной осью
(формулы относятся к движению, несоответствующему оси х; в случае соответствующего движения, следует переставить все факторы, содержащие термин m).
Пример 9
Монтаж на наклонной поверхности (вращение оси z), двойная направляющая, четыре ползуна, отсутствие сил инерции.
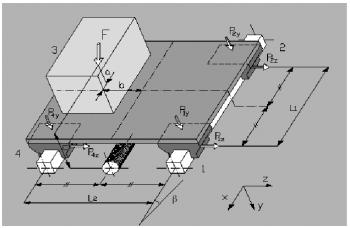 |
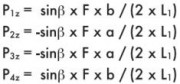 |
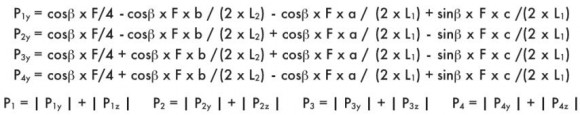
F = нагрузка, действующая в центре тяжести
а = расстояние х между силой F и основной осью
b = расстояние z между силой F и основной осью
с - расстояние у между силой F и основной осью

.png)









 копия.png)