Шарико-винтовые пары (ШВП)

Серия VFU DIN 69051 FORM B >> Стандартная серия Одинарная гайка С фланцем Тип U (DIN 69051) На заказ поставляется с цельным фланцем или со срезом с одной стороны

---

---

Серия WFU DIN 69051 FORM B >> Двойная гайка Стандартная серия С фланцем Тип U (DIN 69051 B) На заказ поставляется с цельным фланцем или со срезом с одной стороны

---

---

Серия VFI >> Одинарная гайка С фланцем Тип I Так же поставляется с левой резьбой

---

---

Серия WFI >> Двойная гайка Тип I Так же поставляется с левой резьбой

---

---

Серия VFE >> Увеличенный шаг резьбы Одинарная гайка С фланцем Стандартно поставляется без уплотнений

---

---

Серия VFK >> Миниатюрная серия d винта от 4 до 25 мм С фланцем от d 4 до 16 не оснащены смазочным отверстием

---

---

Серия VCI >> Гайка без фланца одинарная Тип I Так же поставляется с левой резьбой

---

---

1. Технические характеристики
Шариковые винты, например NBS, отличаются строгим контролем качества, осуществленным во время каждого производственного процесса.
Высокая производительность винтов позволяет снизить крутящий момент до 70 % по отношению к традиционным трапецеидальным винтам, как в применениях общего назначения (превращение вращательного движения в поступательное движение), так и в специальных применениях (превращение поступательного движения во вращательное движение).

1.1 Геометрия контакта
Готическая арка создает значительную прочность винту, одновременно обеспечивая точность и низкие значения крутящего момента.

 

2. Параметры выбора шариковых винтов (с циркуляцией шариков) NBS

Выбор шарикового винта (с циркуляцией шариков) обусловлен следующими параметрами:

-Класс точности

-Шаг резьбы

-Действующая нагрузка

-Номинальный срок службы

-Способ крепления

-Критическая скорость вращения

-Критическая нагрузка

-Жесткость

-Рабочая температура

-Смазка

2.1 Класс точности
В наличии имеются шариковые винты (с циркуляцией шариков) NBS со следующими классами точности:

СО • С1 • С2 • С3 • С5 • С7 • С10

Каждый класс точности обусловлен следующими параметрами:

Е • е • езоо • е2∏

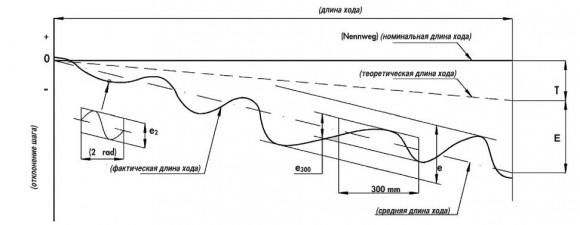
Приведенный ниже график предоставляет описание их значений.

 

 

Таблица - Терминология для обозначения класса точности

Термин	Ссылка	Определение
Компенсация длины хода	Т	Компенсация длины хода -разница между теоретической и номинальной длиной хода; небольшое значение компенсации (если сопоставляется с номинальным ходом) часто необходимо для компенсации удлинения вызванного увеличением температуры или внешними нагрузками. Если в данной компенсации нет необходимости - теоретический ход равен номинальному.
Фактическая длина хода	-	Фактическая длина хода - это осевое смещение между винтом и гайкой.
Средняя длина хода	-	Средняя длина хода - это прямая линия, которая наибольше приближается к фактической длине хода; средняя длина хода представляет собой наклон фактической длины хода.
Отклонение средней длины хода	Е	Отклонение средней длины хода - это разница между средней и теоретической длиной хода.
Изменение хода	е езоо e2п	Изменениями хода называется полоса с двумя параллельными линиями средней длины хода. Максимальный диапазон изменений на длине хода. Диапазон изменений, замеренный на длине обычной части хода равной 300мм. Ошибка биения, диапазон изменений при одном обороте (2 радиана).

 

Таблица - Значения ±Е и e [ед.изм. µм]

Класс точности			С0		С1		С2		С3		С5		С7	С10
Длина хода [мм]	от:	до:	±Е	е	±Е	е	±Е	е	±Е	е	±Е	е	е	е
		100	3	3	3.5	5	5	7	8	8	18	18	±50/ 300mm	±210/ 300mm
	100	200	3.5	3	4.5	5	7	7	10	8	20	18
	200	315	4	3.5	6	5	8	7	12	8	23	18
	315	400	5	3.5	7	5	9	7	13	10	25	20
	400	500	6	4	8	5	10	7	15	10	27	20
	500	630	6	4	9	6	11	8	16	12	30	23
	630	800	7	5	10	7	13	9	18	13	35	25
	800	1000	8	6	11	8	15	10	21	15	40	27
	1000	1250	9	6	13	9	18	11	24	16	46	30
	1250	1600	11	7	15	10	21	13	29	18	54	35
	1600	2000			18	11	25	15	35	21	65	40
	2000	2500			22	13	30	18	41	24	77	46
	2500	3150			26	15	36	21	50	29	93	54
	3150	4000			30	18	44	25	60	35	115	65
	4000	5000					52	30	72	41	140	77
	5000	6300					65	36	90	50	170	93
	6300	8000							110	60	210	115
	8000	10000									260	140
	10000	12500									320	170

 

Таблица - Значения езоо и e2π[ед.изм. µм]

Класс точности	С0	С1	С2	СЗ	С5	С7	С10
езоо	3.5	5	7	8	18	50	210
e2π	2.5	4	5	6	8

 

2.2 Преднатяг и осевой зазор
Преднатяг и осевой зазор шариковых винтов NBS указаны в приведенной ниже таблице.

 

Таблица - Сочетание преднатяга и осевого зазора

Класс преднатяга	Р0	Р1	Р2	РЗ	РА
Осевой зазор	Да	Нет	Нет	Нет	Нет
Преднатяг	Нет	Нет	Легкий	Средний	Сильный

В приведенных ниже таблицах перечисляются основные указания при выборе класса точности, преднатяга и осевого зазора шариковых винтов (с циркуляцией шариков) NBS.

Таблица - Класс точности, преднатяг и осевой зазор

Класс точности	Преднатяг и осевой зазор	Тип гайки	Тип ходового винта
С 10	РО (с осевым зазором)	Одинарная	Накатанный
С 7	Р1 или РО	По требованию	Накатанный или выпрямленный
С 5	По требованию; стандартный 0TNBS-P2	По требованию	Выпрямленный, с сертификатом контроля ошибки шага
С 3	По требованию; стандартный 0TNBS-P2	По требованию	Выпрямленный, с сертификатом контроля ошибки шага

 

Таблица - Макс. осевой зазор для класса преднатяга P0

Номинальный диаметр винта	Накатанный винт	Выпрямленный винт
От 4 мм до 14 мм	0.05 mm	0.015 mm
От 15 мм до 40 мм	0.08 mm	0.025 mm
От 50 мм до 100 мм	0.12 mm	0.05 mm

 

Таблица - Сила преднатяга для класса P2

Модель	Одинарная гайка	Двойная гайка
1605	1 ± 3 N	3 ± 6 N
2005	1 ± 3 N	3 ± 6N
2505	2 ± 5 N	3 ± 6N
3205	2 ± 5 N	5 ± 8N
4005	2 ± 5 N	5 ± 8N
2510	2 ± 5 N	5 ± 8N
3210	3 ± 6 N	5 ± 8N
4010	3 ± 6 N	5 ± 8N
5010	3 ± 6 N	8 ± 12 N
6310	6 ± 10 N	8 ± 12 N
8010	6 ± 10 N	8 ± 12 N

 

 

2.3 Шаг резьбы
Выбор шага винта зависит от следующей формулы:

где:
Ph = шаг винта [мм]
Vmax = максимальная скорость перемещения системы [м/мин]
nmах = максимальный режим вращения винта [мин 1]

В том случае, если результатом уравнения не является целый результат, следует выбрать округленную в большую сторону величину, выбирая между имеющимися в наличии шагами.

2.4 Действующая нагрузка

Учитывая возможную переменность осевых нагрузок, вызванную, например, наличием сил инерции, следует рассчитать значение нагрузки обозначенное, как “средняя динамическая нагрузка Pm”, определяющая одинаковые коэффициенты переменных нагрузок.

2.4.1 Средняя динамическая нагрузка
Для расчета шарикового винта подверженного переменным условиям работы, используются средние значения Рm и nm:

Р_m = средняя динамическая осевая нагрузка[N]
n_m = средняя скорость [мин^-1]

При условиях непрерывной нагрузки и переменной скорости можно достигнуть следующих значений:

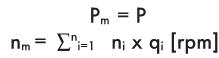
При условиях переменной нагрузки и непрерывной скорости можно достигнуть следующих значений:

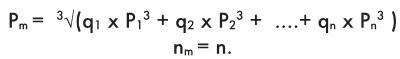
При условиях переменной нагрузки и переменной скорости можно достигнуть следующих значений:

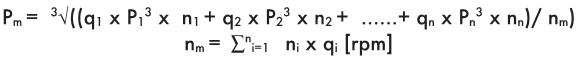
Выбор винта в зависимости от воздействующих и (или) востребованных сил тяги обусловлен следующими величинами:

• Статическая нагрузочная способность Соа
• Динамическая нагрузочная способность Са

2.5 Статическая нагрузка
Нагрузочная статическая способность Соа (или коэффициент нагрузочной способности) определяется в качестве нагрузки постоянной интенсивности, действующей на ось винта, который, в точке максимального воздействия между соприкасающимися частями, устанавливает остаточную деформацию, равную 1/10000 диаметра тела качения.

Значения Соа приведены в размерных таблицах.

 

2.5.1 Коэффициент статического запаса прочности a_s Коэффициент статического запаса прочности a_s (или фактор статического запаса прочности) определяется следующим уравнением:

2.5.2 Коэффициент твердости f_H
Коэффициент твердости учитывает поверхностную твердость дорожек качения:

где:
твердость дорожек HsV10 = фактическая твердость дорожек качения, выраженная в единицах по Виккерсу с испытательной нагрузкой равной 98.07 N

700HV10 = твердость, равная 700 единицам по Виккерсу при испытательной нагрузке равной 98.07 (700HV10 ≈ 60 HRC)

 

Для шариковых винтов NBS следует считать, что f_H = 0.98 ÷1.0 так как винт и маточная гайка имеют поверхностную твердость равную 58 ÷ 62 HRC; для шариков, твердость имеет значение ≥ 60 HRC.

2.5.3 Коэффициент точности f_ac
Коэффициент точности учитывает допуски обработки винта, а значит и класс точности, соответствующий стандарту.
В таблице приведены некоторые примеры.

Таблица - коэффициент f_ac

Класс точности	1 ±5	7	10
fac	1	0.9	0.7

Необходимость в коэффициенте статического запаса прочности a_s > 1 свызвана возможным наличием ударов и (или) вибраций, пусковых и остановочных моментов, случайных нагрузок, которые могут привести к неисправности системы.
В приведенной ниже таблице указаны значения коэффициента статического запаса прочности с учетом типа применения.

Таблица - Коэффициент f_ac

Назначение	Условия	as
Транспорт	Обычные	1.0 ÷ 1.3
	С ударами и (или) вибрацией	2.0 ÷ 3.0
Позиционирование	Обычные	1.0 ÷ 1.5
	С ударами и (или) вибрацией	2.5 ÷ 7.0

2.6 Динамическая нагрузка
Нагрузочной динамической способностью Са (или коэффициентом динамической нагрузки) является постоянная интенсивная динамическая нагрузка, действующая на ось винта, определяющая срок службы 10⁶ оборотов.

Значения С_а приведены в размерных таблицах.

2.7 Номинальный ресурс L

Номинальный ресурс L (это теоретический пробег,выполненный, по крайней мере, 90% показательного количества одинаковых шариковых винтов (с циркуляцией шариков), подверженных одинаковым условиям нагрузкам, не проявляя признаков усталости материала) определяется следующими условиями:

• Гайка без преднатяга
• Гайка с преднатягом

2.7.1 Гайка без преднатяга
Для шариковых винтов (с циркуляцией шариков) с гайкой без преднатяга, расчет номинального ресурса, выраженный в числе оборотов, определяется следующей формулой:

где:
L₁₀ = номинальный ресурс [обороты]
C_a = нагрузочная динамическая способность [N]
P_m = средняя задействованная динамическая осевая нагрузка [N]

Данное уравнение действительно в следующих случаях:
• Твердость дорожек качения = 60HRC
• Класс точности винта от 1 до 5
• Надежность до 90 %

В том случае, если условия эксплуатации не соответствуют приведенным выше условиям, следует использовать следующую формулу:

где:
a₁ = коэффициент надежности
f_ho = коэффициент твердости (см. коэффициент статического запаса прочности a_s)
f_ac = коэффициент точности (см. коэффициент статического запаса прочности a_s)

 

2.7.2 Коэффициент a₁
Коэффициент а₁ учитывает возможность непрогиба C%.

Таблица - Коэффициент возможности непрогиба а₁

C%	80	85	90	92	95	96	97	98	99
a1	1.96	1.48	1.00	0.81	0.62	0.53	0.44	0.33	0.21

Следует заметить, что для С% = 90 a₁= 1.00

2.7.3 Гайка с преднатягом
Действительность последующих формул обусловлена поддержанием постоянного преднатяга; в ином случае следует учитывать случай с гайкой без преднатяга.
Для шариковых винтов (с циркуляцией шариков) с гайкой с преднатягом, расчет номинального ресурса, выраженный в числе оборотов, определяется следующей формулой:

 

где:
L₁₀ = номинальный ресурс [обороты]
L_10a = (C_a/P_m1)³X 10⁶
L_10b - (С_а/Pm₂) х 10⁶

L_10a и L1_0b номинальные ресурсы для двух половинок гайки.

 

Данное уравнение действительно в следующих случаях:
• Твердость дорожек качения = 60HRC
• Класс точности винта от 1 до 5;
• Надежность до 90 %.

В том случае, если условия эксплуатации не соответствуют приведенным выше условиям, следует использовать следующую формулу:

 

где:
L₁₀ = номинальный ресурс [обороты]
L_10a = (C_a/P_m1)³X 10⁶
L_10b - (С_а/Pm₂) х 10⁶

a₁ = коэффициент надежности;
f_ho = коэффициент твердости (см. коэффициент статического запаса прочности a_s)
f_ac = коэффициент точности (см. коэффициент статического запаса прочности a_s)

 

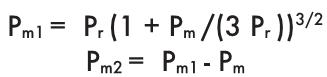
P_m1 и P_m2 - средние осевые динамические нагрузки для двух половинок гайки;

Р_r= сила преднатяга [N]

 

2.7.4 Номинальный срок службы в часах Lh

Имея L₁₀ (номинальныйресурс, выраженный в числе оборотов) можно рассчитать номинальный ресурс в часах работы L_h;

 

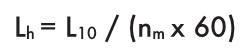
где:
L_m = продолжительность работы [часы]
n_m = средняя скорость вращения [мин^-1]

 

m_i = скорость [МИН^-1]
qi = процентное распределение [%]

 

2.7.5 Номинальный срок службы в км Lkm

 

Имея L₁₀ (номинальный ресурс, выраженный в числе оборотов) можно рассчитать номинальный ресурс пройденного расстояния в км L_km .

где:
L_km=номинальный ресурс [км]
P_h = шаг винта [мм]

В нижеследующей таблице приведены указания типического рабочего ресурса шарикового винта для применений общего назначения.

Таблица - Типичный ресурс шарикового винта

Тип применения	Номинальный ресурс [км]
Контрольно-измерительные машины	250+350
Станки	250
Производственные установки, в общем	150+250
Авиационное оборудование	30

2.8 Способ крепления
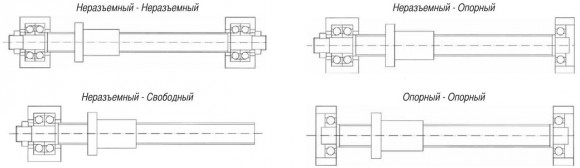
Как правило, существуют следующие типы крепления шарикового винта:

 

Применяемый способ крепления - это функция условий применения, обеспечивающая жесткость и требуемую точность.

2.9 Критическая скорость вращения

Максимальная скорость вращения шарикового винта не должна превышать 80% критической скорости.
Критическая скорость вращения представляет собой точку, в которой винт начинает вибрировать, вырабатывая резонансный эффект, вызванный совпадением частоты вибрации с естественной частотой винта.

Значение критической скорости зависит от внутреннего диаметра ходового винта, способа крепления краев и длины свободной величины прогиба.
Критическая скорость измеряется следующей формулой:

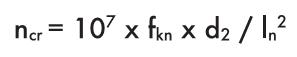
где:
n_cr = критическая скорость [мин^-1]
f_kn = коэффициент способа крепления
d₂ = внутренний диаметр ходового винта [мм]
l_n = длина свободной величины прогиба [мм]

В зависимости от типа крепления, поставляются значения f_kn:

где:
do = номинальный диаметр [мм]
da = диаметр шариков [мм]
а = угол контакта (= 45)

Длина свободной величины прогиба l_n определяется в зависимости от:

-Гайки без преднатяга

l_n = расстояние между креплениями [мм] (в случае крепления “неразъемное - свободное", следует учитывать расстояние между свободным краем винта и гнездом)

 -Гайка с преднатягома

 

l_n = максимальное расстояние между половиной гайки и креплением [мм] (в случае крепления “неразъемное - свободное", следует учитывать максимальное расстояние между половиной гайки и свободным краем винта)

 

n_mах = максимальная скорость вращения винта [обороты/мин]

2.10 Критическая нагрузка

Критическая нагрузка - это максимальная осевая нагрузка, которой может подвергаться винт, не нарушая стабильности системы; в том случае, если действующая на винт максимальная осевая нагрузка достигнет или превысит значение критической нагрузки, создается новая форма воздействия на винт, которое называется “пиковая нагрузка”, вызывающая дополнительный прогиб помимо простого сжатия.

Данное явление, связанное с эластичными свойствами компонента, становиться более чувствительным тогда, когда большая длина свободной величины прогиба винта будет иметь достойные внимание значения по отношению к ее разрезу. Значение критической нагрузки определяется следующей формулой:

где:
P_cr = Критическая нагрузка [N]
f_kp = коэффициент способа крепления
d₂ = внутренний диаметр ходового винта [мм] (см. критическую скорость)
l_cr = длина свободной величины прогиба [мм]

 

В зависимости от типа крепления, поставляются значения fkp:

Неразъемный - Неразъемный	fkр = 40.6
Неразъемный - Опорный	fkp = 20.4
Опорный - Опорный	fkp = 10.2
Неразъемный - Свободный	fkp = 2.6

Для расчета критической нагрузки, значение la определяется максимальным расстоянием между половиной гайки и креплением.

Для большей безопасности, следует рассматривать максимально допустимую осевую нагрузку, как равную половине критической нагрузки:

P_max = максимально допустимая осевая нагрузка [N]

 

2.11 Жесткость

 

Осевая жесткость системы перемещения оснащенной шариковым винтом определяется следующей формулой:

где:
К = осевая жесткость системы [N/µm]
Р = осевая нагрузка [N]
е = осевая деформация системы [µm]

Осевая жесткость системы К - это функция осевой жесткости отдельно взятых компонентов, которые ее составляют: ходовой винт, гайка, опоры, соединительные опорные элементы и гайка.

где:
K_s = осевая жесткость ходового винта [N/µm]
K_N = осевая жесткость гайки [N/µm]
К_в = осевая жесткость опор [N/µm]
К_н = осевая жесткость соединительный опорных элементов и гайки [N/µm]

 

2.11.1 Ks- Осевая жесткость ходового винта

 

Значение жесткости Ks - это функция системы крепления.

Способ крепления: Неразъемный - Неразъемный

где:
d₂ = внутренний диаметр (см. критическую скорость вращения)[mm]
l_s = расстояние между средней осью двух креплений

Способ крепления: Неразъемный - Опорный

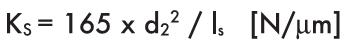
где:
d₂ = внутренний диаметр [мм] (см. критическую скорость )
l_s = максимальное расстояние между средними осями крепления и гайкой [мм].

2.11.2 K_N - Осевая жесткость гайки

Двойная гайка с преднатягом

Значение K_N определяется следующей формулой:

где:
K = табличная жесткость [N/µm]
F_pr = сила преднатяга [N]

 

Простая гайка без преднатяга

 

Значение K_N определяется следующей формулой:

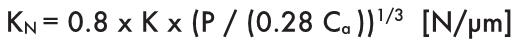
где:
P = осевая нагрузка [N]
C_a = нагрузочная динамическая способность [N]

 

2.11.3 Кв - Осевая жесткость опор

 

Осевая жесткость опор винта обусловлена жесткостью подшипников.
В случае жестких радиальных шариковых подшипников с угловым контактом применяются следующие формулы:

 

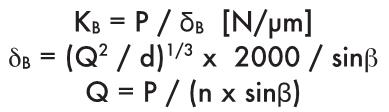
где:
бв = осевая деформация подшипника [N/µm]
Q = нагрузка на каждый шарик [N]
β = угол контакта (45°)
d = диаметр шариков [мм]
N = число шариков

Жесткость соединительных опорных элементов и гаек является характеристикой станка, а значит, не зависит от системы винта, гайки, опор.

2.12 Рабочая температура

 

В случае крепления типа “неразъемный-неразъемный", следует учитывать возможное тепловое расширение, вызванное повышением температуры винта во время работы; такое расширение, если предусмотрено соответствующим образом, оказывает на систему действие дополнительной осевой нагрузки, которое может привести к неисправности работы системы. Для решения проблемы необходимо выполнить достаточный преднатяг винта.

где:
AL = изменения длины [мм] а = коэффициент теплового расширения
(11.7 х 10^-6 [°С^-1])
L = длина винта [мм]
АТ = изменения температуры[°С]

2.13 Смазка

Для смазки шариковых винтов NBS нужно учитывать следующие указания.

2.13.1Смазывание жидким смазочным материалом

Следует предпочитать данный тип смазывания в случае эксплуатации на высоких скоростях вращений. Смазочные